Full Text View
Volume 27 Issue 11 (November 2017)
GSA Today
Article, pp. 6–7 | Abstract | PDF (284KB)

Table of Contents
- Past Earthquake Data
- Earthquake Probability Models
- Implications and Opportunities
- Acknowledgments
- References Cited
Search GoogleScholar
Search GSA Today
GROUNDWORK:
Is the coast toast? Exploring Cascadia earthquake probabilities
1 Dept. of Earth and Planetary Sciences, Northwestern University, and Institute for Policy Research, Northwestern University, Evanston, Illinois 60208, USA
2 Dept. of Earth and Planetary Sciences, Northwestern University, Evanston, Illinois 60208, USA
3 Dept. of Statistics, Northwestern University and Institute for Policy Research, Northwestern University, Evanston, Illinois 60208, USA
The earthquake hazard in the Pacific Northwest due to subduction of the Juan de Fuca plate beneath North America
(Fig. 1A) is drawing much media attention. A The New Yorker article (Schulz, 2015) begins, “An earthquake will destroy a sizable portion of the coastal Northwest. The question is when.” The article quotes a FEMA official saying “everything west of Interstate 5 will be toast.” CBS stated, “Northwest in fear of massive earthquake, tsunami.” NPR reported “Sleeping giant overdue.” Stories include statements like, “In the next 50 years, there is a 1-in-10 chance a ‘really big one’ will erupt,” or, “the odds of the big Cascadia earthquake in the next fifty years are roughly one in three.”
Manuscript received 3 July 2017. Revised manuscript received 29 July 2017. Manuscript accepted 9 Aug. 2017. Posted online 14 Sept. 2017.
10.1130/GSATG350GW.1
©2017, The Geological Society of America.
These stories lead students to ask where these probabilities come from and what they mean, which offers an educational opportunity. Although earthquake probabilities are typically addressed in upper-level classes (Stein and Wysession, 2003; Stein and Stein, 2014), they can be discussed at an introductory level.
Earthquake probability estimates involve two primary choices: which data are used to describe when past earthquakes happened and which models are used to forecast when future earthquakes will happen. These choices’ effects can be illustrated with simple examples.
Past Earthquake Data
Although no large earthquakes occurred along the plate interface for hundreds of years, a record of large paleoearthquakes has been compiled from subsidence data on land and turbidites, offshore deposits recording slope failure. The most recent earthquake occurred in 1700 CE. This record (Fig. 1B) spans 10,000 years, among the world’s longest (Goldfinger et al., 2012, 2013).
(A) Geometry of the Cascadia subduction zone. (B) Paleoearthquake history from turbidite deposits. (C) Probabilities of an earthquake in the next year as a function of time assuming a Gaussian distribution of recurrence times with mean and standard deviation corresponding to the recent cluster (red/dashed lines) or the entire paleoearthquake record (blue/solid lines). Shaded area under the curves corresponds to the probability in next 50 years. (D) Conditional probability of an earthquake in next 50 years, given that last was in 1700, for the four cases discussed.
The recurrence intervals, differences between the dates of successive paleoearthquakes, are key to estimating when the next may occur. The 18 intervals have a mean of 530 years and a standard deviation of 271 years. However, earthquakes seem to have happened in clusters of events, separated by 700–1000-year gaps. The recent cluster covering 1500 years has a mean of 326 years and standard deviation of 88 years. Earthquakes within a cluster occur more frequently and regularly than in the full record. Hence, when to expect the next earthquake depends on whether we assume that we are in the recent cluster, or that the cluster is over.
Earthquake Probability Models
Most students have learned about probability models from games of chance—the chance of a flipped coin coming up heads is 50%. However, earthquake probabilities are more complicated. Despite years of effort, seismologists have not found a good way to describe them. Although many methods are used, all fall into two basic classes.
In one, large earthquakes’ recurrence is described by a time-independent (Poisson) process. This has no “memory,” so a future earthquake is equally likely immediately after the past one and much later. The probability of an earthquake in the next t years is approximately t/τ, where τ is the assumed mean recurrence time. Because this probability is constant, an earthquake cannot be “overdue.” Using the entire paleoearthquake record, the chance of an earthquake in the next 50 years is 50/530 = 0.094 or 9.4%. Alternatively, assuming that we are still in the recent cluster gives a probability about twice as large: 50/326 = 0.15 or 15%.
Time-independent models are used in forecasting floods or hurricanes and in many earthquake hazard studies. However, seismological instincts favor earthquake cycle models, in which strain builds up slowly after an earthquake to produce the next one. In this case, the probability of a large earthquake is small immediately after one occurs and grows with time. In such time-dependent models, the recurrence interval is described by a probability density function. The simplest uses the familiar Gaussian distribution. The “bell curves” in Figure 1C show probabilities of an earthquake in the next year, which peak at dates corresponding to the assumed mean recurrence. Assuming we are in the recent cluster, the probability is high, because the 317 years since 1700 CE is about the mean recurrence of 326 years. The probability is lower assuming that we are not in the cluster, because the mean recurrence for the entire record is 530 years, so we are not as far into the cycle.
To find the probability of an earthquake in 50 years, we integrate under a bell curve from a start time to 50 years in the future, and include the fact that the earthquake hasn’t happened by the start time. The resulting curves (Fig. 1D), called conditional probabilities, are small shortly after 1700 CE and increase with time. Using the entire record, the chance of an earthquake in 50 years after 2017 is 0.074 or 7.4%. However, assuming that we are still in the recent cluster gives a probability ~6 times larger: 0.41 or 41%. The higher probability results from the smaller mean recurrence time and standard deviation.
Figure 1D also shows flat lines starting at 1700 CE, corresponding to time-independent models. If the time-dependent model predicts higher probability than the time-independent model, an earthquake can be considered “overdue,” which occurs if we are in the cluster.
Implications and Opportunities
Comparing these cases shows how earthquake probability estimates depend on the probability model chosen and the data used to choose the model parameters. Other plausible choices are possible. Various probability density functions can be used. The data can be treated in more complex ways: considering different subsets, assigning different magnitudes to different paleoevents, and assuming that different events broke different parts of the subduction zone. Each choice yields a different probability estimate.
A baseball analogy illustrates these ideas. Whether to assume that we are in the cluster is like whether to assume that a hitter’s performance in the next game is better described by his lifetime batting average or by the past few games, because he may be hitting unusually well or in a slump. Choosing between time-independent or time-dependent models is like assuming either that the player’s hitting is the same from year to year or that it changes systematically over his career. The probability of a hit in the next game depends on the assumptions.
There are many opportunities for delving further. Students can explore different assumptions using the data and spreadsheet at www.earth.northwestern.edu/people/seth/Educational/eqprob.html or write spreadsheets or programs using formulations in Stein and Wysession (2003) or Stein and Stein (2014). Instructors or students interested in Cascadia paleoseismology and probabilities can consult Goldfinger et al. (2012). Earthquake probability issues can be explored from discussions in Stark and Freedman (2003), Parsons (2008), Matthews et al. (2002), and Kagan et al. (2012).
The take-home message for students is that saying “the probability of an earthquake is N%” involves specifying the assumptions made. Different plausible assumptions yield different probabilities. This situation may seem frustrating, but it lets instructors explain how limitations in our knowledge give young scientists opportunities for major advances.
Acknowledgments
We thank Michael Hubenthal and three reviewers for helpful comments.
References Cited
- Goldfinger, C., Nelson, C.H., Morey, A.E., Johnson, J.E., Patton, J.R., Karabanov, E., Gutiérrez-Pastor, J., Eriksson, A.T., Gràcia, E., Dunhill, G., Enkin, R.J., Dallimore, A., and Vallier, T., 2012, Turbidite event history—Methods and implications for Holocene paleoseismicity of the Cascadia subduction zone: USGS Professional Paper 1661-F.
- Goldfinger, C., Ikeda, Y., and Yeats, R.S., 2013, Superquakes, supercycles, and global earthquake clustering, 7 Jan. 2013: Earth, https://www.earthmagazine.org/article/superquakes-supercycles-and-global-earthquake-clustering-recent-research-and-recent-quakes (last accessed 17 Aug. 2017).
- Kagan, Y.Y., Jackson, D.D., and Geller, R.J., 2012, Characteristic earthquake model, 1884–2011, R.I.P.: Seismological Research Letters, v. 83, p. 951–953, doi:10.1785/0220120107.
- Matthews, M.V., Ellsworth, W.L., and Reasenberg, P.A., 2002, A Brownian model for recurrent earthquakes: Bulletin of the Seismological Society of America, v. 92, p. 2233–2250, doi:10.1785/0120010267.
- Parsons, T., 2008, Earthquake recurrence on the south Hayward fault is most consistent with a time dependent, renewal process: Geophysical Research Letters, v. 35, doi:10.1029/2008GL035887.
- Schulz, K., 2015, The really big one: The New Yorker, 20 July, p. 20.
- Stark, P.B., and Freedman, D., 2003, What is the chance of an earthquake?, in Mulargia, F., Geller, R.J. eds., Earthquake Science and Seismic Risk Reduction: Dordrecht, Netherlands, Kluwer.
- Stein, S., and Stein, J., 2014, Playing against nature: integrating science and economics to mitigate natural hazards in an uncertain world: Washington, D.C., American Geophysical Union, and New Jersey, Wiley, 278 p.
- Stein, S., and Wysession, M., 2003, Introduction to seismology, earthquakes, and earth structure: New Jersey, Wiley-Blackwell, 510 p.

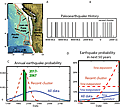 Figure 1
Figure 1