Full Text View
Volume 21 Issue 8 (August 2011)
GSA Today
Article, pp. 4-10 | Abstract | PDF (3.7MB)
Understanding Earth’s eroding surface with 10Be
| Table of Contents |
|---|
|
Search GoogleScholar for
Search GSA Today |
Abstract
For more than a century, geologists have sought to measure the distribution of erosion rates on Earth’s dynamic surface. Since the mid-1980s, measurements of in situ 10Be, a cosmogenic radionuclide, have been used to estimate outcrop and basin-scale erosion rates at 87 sites around the world. Here, we compile, normalize, and compare published 10Be erosion rate data (n = 1599) in order to understand how, on a global scale, geologic erosion rates integrated over 103 to 106 years vary between climate zones, tectonic settings, and different rock types.
Drainage basins erode more quickly (mean = 218 m Myr−1; median = 54 m Myr−1) than outcrops (mean = 12 m Myr−1; median = 5.4 m Myr−1), likely reflecting the acceleration of rock weathering rates under soil. Drainage basin and outcrop erosion rates both vary by climate zone, rock type, and tectonic setting. On the global scale, environmental parameters (latitude, elevation, relief, mean annual precipitation and temperature, seismicity, basin slope and area, and percent basin cover by vegetation) explain erosion rate variation better when they are combined in multiple regression analyses than when considered in bivariate relationships. Drainage basin erosion rates are explained well by considering these environmental parameters (R2 = 0.60); mean basin slope is the most powerful regressor. Outcrop erosion rates are less well explained (R2 = 0.32), and no one parameter dominates. The variance of erosion rates is better explained when subpopulations of the global data are analyzed. While our compilation is global, the grouped spatial distribution of cosmogenic studies introduces a bias that will only be addressed by research in under-sampled regions.
*E-mails: ,
Manuscript received 27 Oct. 2010; accepted 1 Apr. 2011
DOI: 10.1130/G111A.1
INTRODUCTION
Accurate global mapping, understanding, and prediction of geologic or background erosion rates is important because erosion is the means by which sediment is generated, fresh rock is exposed to CO2-consuming weathering reactions, soil is created, landforms change over time, and mass is moved from the continents to the oceans and eventually recycled via the process of subduction and volcanism. Earth’s ability to support billions of inhabitants depends critically on the resiliency of the soil system and the purity of surface waters, both of which erosion affects directly. Thus, measuring the rate and spatial distribution of erosion on millennial time scales is fundamental to understanding how landscapes evolve through time and for placing human environmental impacts in context (Hooke, 1994, 2000).
Yet, geoscientists are largely lacking the data to develop a global model that can predict, with accuracy or precision, the background rate and spatial distribution of erosion on Earth’s dynamic surface. It is even more difficult to predict how erosion rates respond to changes in boundary conditions including tectonic and climatic forcing. Understanding how rates of erosion are related to complex, non-linear feedbacks between multiple Earth systems including the solid Earth (tectonic regime), the climate (precipitation and temperature), and the biosphere (vegetation) is prerequisite to developing such a model.
Throughout the twentieth century, geologists used a variety of tools to measure rates of erosion (e.g., Saunders and Young, 1983). The most common approach equated sediment yield with erosion rate (Dole and Stabler, 1909; Judson, 1968). Such an approach presumes that human impact is inconsequential and that short-term measurements of sediment flux are representative of long-term flux rates, but both assumptions have been repeatedly questioned (e.g. Kirchner et al., 2001; Trimble, 1977; Wilkinson, 2005), and various modeling approaches have been implemented (Syvitski et al., 2005) to overcome the limitations of sediment yield data.
Geologic erosion rates are useful for placing human impact on the sedimentary system and global environment in context. Until recently, no one method of measuring geologic erosion rates directly was globally applicable. The development of Accelerator Mass Spectrometry (AMS) allowed rapid, high-precision, low-detection limit measurement of in situ–produced cosmogenic radionuclides (Elmore and Phillips, 1987), the concentration of which reflects near-surface residence time and thus the pace of surface processes (Bierman and Nichols, 2004). In situ–produced 10Be, extracted from purified quartz, is now routinely used to estimate how quickly outcrops and drainage basins erode over geomorphically meaningful time scales (e.g., Bierman and Caffee, 2001; Bierman and Steig, 1996; Brown et al., 1995; Granger et al., 1996; Nishiizumi et al., 1986; Schaller et al., 2001; Small et al., 1997).
The method relies on the observation that cosmic rays interact with Earth’s surface, producing 10Be, an otherwise exceptionally rare isotope. The production of 10Be occurs predominantly within a few meters of Earth’s surface and decreases exponentially with depth. Thus, the concentration of 10Be in outcropping rock or in fluvial sediment reflects near-surface residence time. Cosmogenic rate estimates reflect the time it takes to erode several meters of rock or sediment, typically 103 to 106 years, the integration time being inversely proportional to the erosion rate. In bedrock outcrops, erosion rates are inferred, assuming erosion occurs steadily through time. Sampling river sand presumes that stream networks mix and deliver sediment from the entire basin. Because soils are typically well-stirred by physical and biological processes, shallow, human-induced soil erosion does not typically affect cosmogenic estimates of basin-scale erosion rates.
Many local and regional-scale cosmogenic studies (now 87) indicate that individual environmental parameters can influence millennial-scale erosion rates, although the results are not uniform. Parameters considered in the past include latitude, elevation, relief, seismicity, basin slope and area, percent basin cover by vegetation, and mean annual precipitation and temperature. In order to understand the relationship between erosion rates and environmental parameters, we compiled all publicly available outcrop and drainage basin erosion rates inferred from measurements of 10Be (Fig. 1). After standardizing the data for changes in 10Be half-life (Nishiizumi et al., 2007), production rate (Balco et al., 2008), and scaling schemes (Lal, 1991) used over the past 24 years, we compared erosion rates and a variety of environmental parameters, both individually and using multivariate statistical methods. The result is a description, at a global scale, of the relationship between these parameters and the erosion rate of both outcrops and drainage basins. Such relationships are important for understanding the behavior of Earth’s sedimentary system over a variety of spatial and temporal scales as geologists attempt to make sense of human impacts on erosion and sediment generation (Hooke, 1994; Montgomery, 2007; Wilkinson, 2005).
|
Geographical distribution of cosmogenic 10Be erosion rate data (see supplemental data Tables DR1–DR3 [see text footnote 1]). (A) Location of studies compiled in this paper. (B) Distribution of outcrop samples and (C) drainage basin samples. Symbols sized to reflect the number of samples per study and colored to indicate relative erosion rate. Note: Citations included within this figure are listed with the supplemental data text. |
We recognize that a spatial bias introduced to our analyses is due to the small number of studies carried out in South America, Africa, the Middle East, and the polar latitudes as well as the fact that the number of samples from each study varied in size. Our compilation and analyses are carried out using available data, however, and further sampling in under-studied regions can only improve our understanding of how different factors control erosion rates.
Methods
We compiled all publicly available in situ 10Be erosion rate data (Fig. 1; Tables DR1–DR3 1 ). We included only unshielded outcropping bedrock samples collected from horizontal or subhorizontal surfaces and modern stream sediment samples from drainage basins that did not experience extensive recent glacial cover. For each sample, we collected data necessary to recalculate erosion rates (Table DR1). In some cases, information was provided in the original publications; in other cases, we contacted authors directly. Samples in this compilation required recalculation because constraints on production rates, neutron attenuation path length, and the 10Be half-life have improved over time and values used in individual studies varied widely.
1GSA supplemental data item 2011216, reference list for text Figure 1, erosion rate recalculation methods, ArcGIS data extraction methods, statistical methods, results of statistical analyses (including Figs. DR1–DR4), and bedrock and drainage basin erosion rate data tables (Tables DR1–DR5), is online at www.geosociety.org/pubs/ft2011.htm. You can also request a copy from GSA Today, P.O. Box 9140, Boulder, CO 80301-9140, USA; .
We used the CRONUS online calculator for erosion rate estimates (Balco et al., 2008; hess.ess.washington.edu). Effective elevation, or the production-rate weighted average elevation for a basin, and effective latitude were determined (see supplemental data methods section [footnote 1]), enabling us to use the CRONUS calculator for determining drainage basin erosion rates. CRONUS-calculated erosion rates for outcrops and basins strongly and significantly correlate to their original published erosion rates (Figure DR1).
We compared erosion rates for outcrops and drainage basins to latitude (°N or °S), elevation (meters above sea level [masl]), mean annual precipitation (MAP; mm yr−1) and temperature (MAT; °C), seismicity (peak ground acceleration [PGA; see supplemental data {footnote 1}], where seismically active sites have PGA >2), basin area (km2), mean basin slope (°), and percent basin coverage by vegetation. These parameters are used because they are the most commonly analyzed metrics in cosmogenic erosion rate literature to date. We extracted data from global datasets using ArcGIS (Table DR4). Not all global coverages extend to Antarctica. Antarctic climate data were modified from Monaghan et al. (2006), and because seismicity data were not available for Antarctica, those sites are excluded from some of our analyses. See the supplemental data for details regarding these parameters.
We used a variety of statistical methods (see supplemental data [footnote 1]). These parametric statistical tests assume a normal sample distribution. Because both outcrop and drainage basin erosion rate distributions are highly skewed (Fig. 2), we log-transformed (base 10) all erosion rate data before performing statistical tests; this transformation produced a more normally distributed dataset. Bivariate analyses were carried out for numeric parameters, and we completed analyses of variance and Student’s t-Tests for nominal data. We also performed forward stepwise regressions for each global dataset and for each subgroup of nominal data categories. Parameters were entered into the regression based on their ability to statistically improve the regression. If a variable did not significantly improve the regression, it was omitted.
|
Erosion rate data. (A) Exceedance probability for compiled erosion rates. (B) Histogram of outcrop erosion rates. (C) Histogram of drainage basin erosion rates. (D) Histograms of erosion rates after being log-transformed (base 10) showing normally distributed datasets for statistical analyses; outcrops are green lines and drainage basins are red lines. |
Results
Outcrop Erosion Rates
Outcrops (n = 450) erode at an average rate of 12 ± 1.3 m Myr−1. The median erosion rate is 5.4 m Myr−1, reflecting the highly skewed distribution (Fig. 2B). In bivariate global comparisons (Fig. DR2), outcrop erosion rates are unrelated to absolute latitude, elevation, or seismicity. Globally, outcrop erosion rates co-vary weakly with relief and MAP; the highest outcrop erosion rates occur where MAT is ~10 °C.
Analysis of variance (ANOVA) shows that outcrops in seismically active regions erode similarly (14 ± 1.6 m Myr−1; n = 55) to those in seismically inactive areas (13 ± 1.4 m Myr−1; n = 395) but that outcrop erosion rates differ by lithology and climate (Fig. 3). Erosion rates of sedimentary (20 ± 2.0 m Myr−1; n = 118) outcrops are faster than metamorphic outcrops (11 ± 1.4 m Myr−1; n = 102) and igneous outcrops (8.7 ± 1.0 m Myr−1; n = 230), which are statistically similar. The average outcrop erosion rate in temperate climates (25 ± 2.5 m Myr−1; n = 85) is significantly higher than those in any other climate zone except for erosion rates in tropical zones. Outcrops in polar climates erode most slowly (3.9 ± 0.39 m Myr−1; n = 31). Median values show similar trends (Fig. 4).
|
Analysis of variance (ANOVA) for the log-transformed CRONUS erosion rates on outcrop and drainage basin samples categorized by rock type, climate zone, and tectonic regime. Letters below each box-plot represent the results from paired Student’s t-Tests—categories linked by a similar letter are similar at p <0.05. Green lines are means; red lines are medians. Box defines 25th and 75th percentiles. Whiskers represent data range, excluding statistical outliers. |
|
Forward stepwise regressions for outcrop and drainage basin datasets considered globally and by subdivisions of categorical data. Colored boxes indicate parameters that significantly explain erosion rate variance. The number in each colored box is the amount of the overall R2 value contributed by the corresponding parameter. The R2 value listed at the bottom of each column represents the total amount of variation in the data that is explained by the significant parameters. Regressions use log-transformed CRONUS erosion rates. Mean and median values calculated from CRONUS erosion rates. |
A forward stepwise regression shows that 32% of the variation in the global population of outcrop erosion rates can be described by five parameters; MAP is the most important regressor (Fig. 4). For individual climate zones, lithologies, and seismic regimes, the relevant parameters and their weighting vary greatly (Fig. 4; Table DR5).
Drainage Basin Erosion Rates
On average, sampled drainage basins erode at 218 ± 35 m Myr−1 (n = 1149). The distribution is highly skewed, with a median erosion rate of 54 m Myr−1 (Fig. 2C). At the global scale, basin slope yields the strongest bivariate correlation, with erosion rates (R2 = 0.33, Fig. 5; Fig. DR3). Basin relief, mean elevation, and seismicity also have significantly positive, bivariate correlations. MAT has a very weak negative correlation. There is no significant bivariate correlation between basin erosion rates and latitude, MAP, or basin area (Fig. DR3).
|
Mean basin slope and erosion rate co-vary. Correlation is scaledependent and decreases with increasing area included in the sample: Appalachian Plateau within the Susquehanna River Basin (red squares; Reuter, 2005); Appalachian Mountains crest data (green triangles; Matmon et al., 2003; Reuter, 2005; Sullivan, 2007); and global data set (gray circles; references in Table DR1 [supplemental data; see text footnote 1]). |
Analysis of variance (Fig. 3) indicates that the average erosion rate for seismically active basins (367 ± 55 m Myr−1; n = 221) is significantly higher than in seismically inactive basins (182 ± 30 m Myr−1; n = 928). The average drainage basin erosion rate in polar climates (537 ± 125 m Myr−1; n = 71) is higher than in all other climate zones. Arid region drainage basins erode most slowly (100 ± 17.3 m Myr−1; n = 229). Results are less clear for lithology. On average, metamorphic terrains erode more rapidly than other lithologies, but this is not reflected in ANOVA results on log-transformed data (Fig. 3).
Forward stepwise regressions of basin erosion rates show that all nine parameters together significantly describe 60% of variability in the global data set (Fig. 4). For nearly every basin-scale subcategory, basin slope is the most significant regressor (Fig. 4). The remaining parameters are highly variable in terms of their regression power. Basin area, MAT, and elevation have low weights for nearly all subcategories in which they appear.
Discussion
While summaries of 10Be erosion rate data have been presented in the past (e.g., Bierman and Nichols, 2004; von Blanckenburg, 2005), our compilation of 1599 measurements of in situ–produced 10Be provides the first broad, standardized view of pre-human, geologic erosion rates (Figs. 1 and 2). Compiled outcrop erosion rates are slow and do not exceed 140 m Myr−1, similar to rock weathering rates measured in the past (Saunders and Young, 1983). Some cosmogenic studies in tectonically active zones (i.e., Binnie et al., 2006, 2008; DiBiase et al., 2009) indicate drainage basin erosion rates higher than previously reported (Saunders and Young, 1983).
Spatial Distribution of Existing Samples
Our compilation is global; however, large portions of Earth remain unsampled, meaning that the data are not randomly distributed (Fig. 1). Drainage basin cosmogenic data represent only 2.3% of the world’s land area. Latitudes with large sample populations, between 30°–50° north and south, correspond to Europe, the United States, and Australia—easily accessible locations. There are sampling gaps between 50°–70° latitude, both north and south. Low latitude samples are also rare. Exceptions include large sample populations from basins and outcrops in Namibia and the Bolivian Andes (i.e., Bierman and Caffee, 2001; Cockburn et al., 2000; Insel et al., 2010; Kober et al., 2007, 2009; Safran et al., 2005; Wittmann et al., 2009). Refining the relationships presented in this study will happen only when these large spatial data gaps are filled.
Both outcrop and drainage basin erosion rates have highly skewed distributions (Fig. 2), with most samples indicating relatively slow rates of erosion. This skewed distribution probably reflects the rapidity of erosion in tectonically active zones where mass is supplied to orogens by plate convergence and removed by rapid erosion of threshold slopes (Montgomery and Brandon, 2002; Zeitler et al., 2001). In contrast, slower, isostatically driven rock uplift supplies mass for erosion in the tectonically stable zones that make up most of the world (Hack, 1975, 1979).
Studies with a large number of samples in one region (i.e., Bierman and Caffee, 2002; DiBiase et al., 2009; Henck et al., 2011; Ouitmet et al., 2009; Safran et al., 2005; Schaller et al., 2001) are helpful in creating large sample populations for statistical analyses; however, sample adjacency leads to biases in data interpretation because of the scale dependence of correlation. For example, outcrops in “cold” climates come from numerous locations geographically (n = 108), and the stepwise multivariate regression accounts for only 2% of the variability of erosion rates, whereas 52% of variability of erosion rates in “polar” climates is explained (Fig. 4). This high correlation is most likely the result of all 31 polar outcrop samples coming from a single, small geographic area.
Most 10Be measurements have been done in quartz-rich rocks and sediment because quartz retains in situ 10Be and has a simple composition, so nuclide production rates are easily calculated. Not all rocks are quartz-bearing; thus, the global data set does not represent all lithologies. Beryllium-10 can be extracted from other minerals (Ivy-Ochs et al., 2007; Nishiizumi et al., 1990), expanding the area where erosion rates can be measured. Application of other isotope systems (such as 21Ne, 3He, and 36Cl) offers the potential to better constrain the effect of lithology on erosion rates (Kober et al., 2009); however, uncertainties in cross calibration of production rates between different isotope systems could introduce biases into the data analysis.
Basins Erode More Rapidly Than Outcrops
Average outcrop erosion rates are more than fifteen times slower (12 m Myr−1) than those inferred from drainage basin studies (218 m Myr−1). Comparison of median and outcrop drainage basin rates (5.3 vs. 54 m Myr−1, respectively) shows a similar relationship. Within each seismic regime, climate zone, and lithology, drainage basins erode more rapidly than outcrops (Fig. 4). There are 22 sites or regions where both outcrop and basin erosion rates have been measured (Fig. DR4). At 12 of these, statistical analyses indicate that drainage basins erode more rapidly than outcrops; at the other 10 sites, drainage basin and outcrop erosion rates are statistically inseparable. In no case, does a Student’s t-Test indicate that outcrops erode more rapidly than the adjacent basins. These results suggest that soil cover, even if it is quite shallow, speeds the rate of rock weathering (Heimsath et al., 1997, 1999).
Outcrop and drainage basin erosion rates are controlled by different processes and occur in different physical, chemical, and hydrological environments. Outcrops are situated above the landscape and exposed to a limited suite of what must be largely ineffective subaerial erosion processes that both physically and chemically wear away exposed rock. The stability of outcrops is likely due to the dry microclimate they create as precipitation rapidly runs off exposed rock surfaces. The conversion of bedrock to regolith results from linked chemical and physical processes that include hydrolysis, weathering induced by organic acids, and the ability of soil to hold water in contact with rock between precipitation events. A mantle of soil appears to create conditions favorable for the conversion of bedrock to soil (Heimsath et al., 1997, 1999).
Influence of Spatial Scale on Erosion Rate Correlation
Scale appears to determine which environmental parameters are related to outcrop and drainage basin erosion rates because correlations observed on the local scale are often not observed or are much weaker on the global scale. For example, in Australia, the lowest measured outcrop erosion rate from sampling sites on Australia’s Eyre Peninsula and in central Australia correlate well with MAP (R2 = 0.98; Bierman and Caffee, 2002). On the global scale, however, this relationship is much weaker (Fig. DR2E). Drainage basin erosion rates have previously been shown to correlate well with average basin elevation in individual studies (Heimsath et al., 2006; Palumbo et al., 2009). This bivariate relationship is weak at the global scale (R2 = 0.14; Fig DR3B), and elevation is at most a lightly weighted regressor in all of the multivariate regressions (Fig. 4), suggesting that, on a global scale, elevation is not an important control on erosion rates.
Mean basin slope is the one parameter that is significantly related to drainage basin erosion rates at both the local (e.g., DiBiase et al., 2009; Matmon et al., 2003; Ouimet et al., 2009; Palumbo et al., 2009; von Blanckenburg et al., 2004) and global level. However, scale remains important. For example, mean basin slope produced the strongest bivariate correlation (Fig. 5) with drainage basin erosion rates at the global scale (total basin area = 3.3 × 106 km2, R2 = 0.34). The regression explains more variability if only the Appalachian Mountain crest data are included (6.9 × 104 km2, R2 = 0.49) and gets even better if the data included are restricted to the Appalachian Plateau (786 km2, R2 = 0.75). Although bivariate analysis may be useful at local and regional scales, such regressions are of lesser value at global scales. Multivariate analysis is needed because many environmental metrics, such as slope, relief, elevation, and MAP, spatially co-vary.
Correlation of Physical and Environmental Parameters to Erosion Rates
Compiling and analyzing the global 10Be dataset shows that the most successful understanding of erosion rates, in the absence of site-specific studies, will come from multivariate analyses of drainage basin data (Fig. 4; Table DR5). In general, analysis of data by climatic, tectonic, or lithologic subpopulations provides better correlation (higher R2 value) because of the autocorrelation of erosion rates within similar process domains. Multivariate analysis explains almost twice as much variance in drainage basin erosion rates as in outcrop erosion rates, suggesting that there are other, unconsidered parameters controlling outcrop erosion rates (such as rock strength, structure, and joint spacing). Collecting such data along with samples for cosmogenic analysis would likely improve the understanding of controls on exposed bedrock erosion rates.
Some physical drainage-basin metrics, such as relief and slope, are clearly related both to each other and to drainage basin erosion rates. On the global scale, relief and slope both produced significant bivariate correlations with drainage basin erosion rates. In the multivariate analyses, slope was the predominant regressor in nearly every subdivision of categorical data (Fig. 4), as well as for the global basin-scale multivariate regression. Relief is unimportant for most categories of outcrops, except for sedimentary rocks and tropical climate zones. The lack of a relationship between watershed area and 10Be-estimated drainage basin erosion rates is important because it indicates that changes in the sediment delivery ratio do not affect estimation of erosion rates cosmogenically; this finding stands in stark contrast to estimates made on the basis of sediment yield (Trimble, 1977; Walling, 1983).
Seismicity, a proxy for tectonics, is positively related to drainage basin erosion rates in bivariate regression, multivariate regressions, and in the comparison of tectonically active and inactive basins (Fig. 4; Fig. DR4). This relationship has previously been observed (i.e., von Blanckenburg, 2005) and likely reflects tectonic weakening of rocks through seismic shaking, deformation, fracturing, and perhaps base-level lowering (Riebe et al., 2001b). Multivariate regressions for both outcrops and basins in tectonically active areas show high R2 values.
Although individual climate metrics are weakly related to erosion rates (Fig. 4), consistent with the findings of Reibe et al. (2001a), erosion rates of both outcrops and basins vary significantly by climate zone (Fig. 3). MAP is frequently cited as a parameter controlling erosion rates and a relationship is often observed in local and regional studies of both outcrop and drainage basin erosion (e.g., Bierman and Caffee, 2002, 2001; Henck et al., 2011; von Blanckenburg et al., 2004). Although MAP may produce a strong correlation at the local scale, the weak correlations observed globally and with multivariate analyses suggest MAP does not play an important role in explaining erosion rates for most basins. MAT is a significant regressor for polar basins; otherwise, its weighting is usually low (Fig. 4). MAT carries high weighting for some subcategories of outcrops. Latitude, a climate proxy, is significant in most basin subcategories. The percentage of a drainage basin covered with vegetation is generally unimportant.
Implications for Landscape Evolution
The greater than ten-fold offset between rates of outcrop erosion and those of drainage basins suggests that ridgelines, where outcrops are most common, erode less rapidly than surrounding basins. Taken at face value, the offset between outcrop and drainage basin erosion rates is consistent with increasing relief, which may be driven by base-level changes (Riebe et al., 2001b), the result of Pleistocene sea-level changes, or by repeated climate swings (Peizhen et al., 2001). By collecting from the tops of bedrock outcrops, geologists sample the most stable portions of the landscape; perhaps then, it is no surprise that isolated outcrops erode more slowly than basins as a whole. However, this erosion rate offset cannot continue forever because ridgelines will eventually be consumed from their margins by the more rapidly eroding basins.
Cosmogenic data show that millennial-scale erosion rates differ between climate zones. Substituting time for space, glacial-interglacial climate cycles probably changed erosion rates and thus the flux of sediment shed off the landscape. Erosion rates are generally high for both outcrops and basins in temperate and cold climate zones, peaking where the MAT is ~10 °C (Figs. DR2–DR3). Temperatures in these climate zones fluctuate throughout the year, with numerous freeze-thaw cycles that may facilitate frost cracking on outcrops and cryoturbation on basin hillslopes (Delunel et al., 2010; Hales and Roering, 2007). This hypothesis is testable. Paleo-erosion rates should be higher than modern rates in warmer climate locations that cooled significantly during the Pleistocene.
Conclusions and Future Prospects
Compiling more than 20 years of cosmogenic analyses clearly shows their value in measuring background rates of erosion around the world, understanding how such rates are related to environmental parameters, and laying the groundwork for predicting long-term sediment generation rates at a variety of spatial scales. Yet, the same compilation demonstrates spatial biases in the existing data set, providing both justification and guidance for filling these data gaps. Multivariate regressions, using widely available environmental data, explain much of the variance in drainage basin erosion rates. Outcrop erosion rates are less well explained, suggesting that important controlling parameters, such as fracture density, joint spacing, bedrock structure, and rock strength and chemistry, need to be measured and considered in any predictive model.
Acknowledgments
This work was inspired by and builds upon a similar compilation started by J. Reuter (2005). We thank L. Reusser, whose help with script-writing was paramount to this paper, D. Rizzo for statistical consulting, the 2010 UVM Critical Writing seminar for editing, and three reviewers, including E. Kirby, M. Oskin, and A. Henck. Data compilation, analysis, and writing were supported in part by U.S. NSF grants EAR-310208 and ARC-1023191.
REFERENCES CITED
Editor’s note: References for the 82 citations in Figure 1 of this paper have been included with the online supplemental data (see footnote 1).
- Balco, G., Stone, J.O., Lifton, N.A., and Dunai, T.J., 2008, A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements: Quaternary Geochronology, v. 3, p. 174–195.
- Bierman, P.R., and Caffee, M.W., 2001, Slow rates of rock surface erosion and sediment production across the Namib Desert and escarpment, Southern Africa: American Journal of Science, v. 301, no. 4–5, p. 326–358.
- Bierman, P.R., and Caffee, M.W., 2002, Cosmogenic exposure and erosion history of ancient Australian bedrock landforms: Geological Society of America Bulletin, v. 114, no. 7, p. 787–803.
- Bierman, P.R., and Nichols, K.K., 2004, Rock to sediment—slope to sea with 10Be—rates of landscape change: Annual Reviews of Earth and Planetary Sciences, v. 32, p. 215–255.
- Bierman, P.R., and Steig, E., 1996, Estimating rates of denudation and sediment transport using cosmogenic isotope abundances in sediment: Earth Surface Processes and Landforms, v. 21, p. 125–139.
- Binnie, S.A., Phillips, W.M., Summer?eld, M.A., and Fi?eld, L.K., 2006, Sediment mixing and basin-wide cosmogenic nuclide analysis in rapidly eroding mountainous environments: Quaternary Geochronology v. 1, p. 4–14.
- Binnie, S.A., Phillips, W.M., Summer?eld, M.A., Fi?eld, L.K., and Spotila, J.A., 2008, Patterns of denudation through time in the San Bernardino Mountains, California: Implications for early-stage orogenesis: Earth and Planetary Science Letters, v. 276, no. 1–2, p. 62–72.
- Brown, E.T., Stallard, R.F., Larsen, M.C., Raisbeck, G.M., and Yiou, F., 1995, Denudation rates determined from the accumulation of in situ-produced 10Be in the Luquillo Experimental Forest, Puerto Rico: Earth and Planetary Science Letters, v. 129, p. 193–202.
- Cockburn, H.A.P., Brown, R.W., Summerfield, M.A., and Seidl, M.A., 2000, Quantifying passive margin denudation and landscape development using a combined fission-track thermochronology and cosmogenic isotope analysis approach: Earth and Planetary Science Letters, v. 179, no. 3–4, p. 429–435.
- Delunel, R., van der Beek, P. A., Carcaillet, J., Bourlès, D.L., and Valla, P.G., 2010, Frost-cracking control on catchment denudation rates: Insights from in situ produced 10Be concentrations in stream sediments (Ecrins-Pelvoux massif, French Western Alps): Earth and Planetary Science Letters, v. 293, p. 72–83.
- DiBiase, R.A., Whipple, K.X., Heimsath, A.M., and Ouimet, W.B., 2009, Landscape form and millennial erosion rates in the San Gabriel Mountains, CA: Earth and Planetary Science Letters, v. 289, p. 134–144.
- Dole, R.B., and Stabler, H., 1909, Denudation: USGS Water Supply Paper, v. 234, p. 78–93.
- Elmore, D., and Phillips, F., 1987, Accelerator mass spectrometry for measurement of long-lived radioisotopes: Science, v. 236, p. 543–550.
- Granger, D.E., Kirchner, J.W., and Finkel, R., 1996, Spatially averaged long-term erosion rates measured from in situ-produced cosmogenic nuclides in alluvial sediments: Journal of Geology, v. 104, no. 3, p. 249–257.
- Hack, J.T., 1975, Dynamic equilibrium and landscape evoluion, in Melhorn, W.N., and Flemal, R.C., eds., Theories of landform development: Binghamton, New York, SUNY, p. 87–102.
- Hack, J.T., 1979, Rock control and tectonism, their importance in shaping the Appalachian highlands: U.S. Geological Survey Professional Paper 1126B, p. 17.
- Hales, T.C., and Roering, J.J., 2007, Climatic controls on frost cracking and implications for the evolution of bedrock landscapes: Journal of Geophysical Research, v. 112, no. F02033, p. 14.
- Heimsath, A.M., Dietrich, W.E., Nishiizumi, K., and Finkel, R.C., 1997, The soil production function and landscape equilibrium: Nature (London), v. 388, no. 6640, p. 358–361.
- Heimsath, A.M., Dietrich, W.E., Nishiizumi, K., and Finkel, R.C., 1999, Cosmogenic nuclides, topography, and the spatial variation of soil depth: Geomorphology, v. 27, no. 1–2, p. 151–172.
- Heimsath, A.M., Chappel, J., Finkel, R.C., Fifield, K., and Alimanovic, A., 2006, Escarpment erosion and landscape evolution in southeastern Australia, in Willett, S.D., Hovius, N., Brandon, M.T., and Fisher, D.M., eds., Tectonics, Climate, and Landscape Evolution: Geological Society of America Special Paper 398, p. 173–190.
- Henck, A.C., Huntington, K.W., Stone, J.O., Montgomery, D.R., and Hallet, B., 2011, Spatial controls on erosion in the Three Rivers Region, southeastern Tibet and southwestern China: Earth and Planetary Science Letters, v. 303, p. 71–83.
- Hooke, R.L., 1994, On the efficacy of humans as geomorphic agents: GSA Today, v. 4, no. 9, p. 217, 224–225.
- Hooke, R.L., 2000, On the history of humans as geomorphic agents: Geology, v. 28, no. 9, p. 843–846.
- Insel, N., Ehlers, T.A., Schaller, M., Barnes, J.B., Tawackoli, S., and Poulsen, C.J., 2010, Spatial and temporal variability in denudation across the Bolivian Andes from multiple geochronometers: Geomorphology, v. 122, p. 65–77.
- Ivy-Ochs, S., Kober, F., Alfimov, V., Kubik, P.W., and Synal, H.-A., 2007, Cosmogenic 10Be, 21Ne and 36Cl in sanidine and quartz from Chilean ignimbrites: Nuclear Instruments and Methods in Physics Research B, v. 259, p. 588–594.
- Judson, S., 1968, Erosion of the land or what’s happening to our continents: American Scientist, v. 56, p. 356–374.
- Kirchner, J.W., Finkel, R.C., Riebe, C.S., Granger, D.E., Clayton, J.L., King, J.G., and Megahan, W.F., 2001, Mountain erosion over 10 yr, 10 k.y., and 10 m.y. time scales: Geology, v. 29, no. 7, p. 591–594.
- Kober, F., Ivy-Ochs, S., Schlunegger, F., Baur, H., Kubik, P.W., and Wieler, R., 2007, Denudation rates and a topography-driven rainfall threshold in northern Chile: Multiple cosmogenic nuclide data and sediment yield budgets: Geomorphology, v. 83, p. 97–120.
- Kober, F., Ivy-Ochs, S., Zeilinger, G., Schlunegger, F., Kubik, P.W., Baur, H., and Wieler, R., 2009, Complex multiple cosmogenic nuclide concentration and histories in the arid Rio Lluta catchment, northern Chile: Earth Surface Processes and Landforms, v. 34, p. 398–412.
- Lal, D., 1991, Cosmic ray labeling of erosion surfaces; in situ nuclide production rates and erosion models: Earth and Planetary Science Letters, v. 104, no. 2–4, p. 424–439.
- Matmon, A.S., Bierman, P., Larsen, J., Southworth, S., Pavich, M., Finkel, R., and Caffee, M., 2003, Erosion of an ancient mountain range, the Great Smoky Mountains, North Carolina and Tennessee: American Journal of Science, v. 303, p. 817–855.
- Monaghan, A.J., Bromwich, D.H., and Wang, S.-H., 2006, Recent trends in Antarctic snow accumulation from Polar MM5 simulations: Philosophical Transactions of the Royal Society London A, v. 364, p. 25.
- Montgomery, D.R., 2007, Is agriculture eroding civilization’s foundation?: GSA Today, v. 17, no. 10, p. 4–9.
- Montgomery, D.R., and Brandon, M.T., 2002, Topographic controls on erosion rates in tectonically active mountain ranges: Earth and Planetary Science Letters, v. 201, no. 3–4, p. 481–489.
- Nishiizumi, K., Lal, D., Klein, J., Middleton, R., and Arnold, J.R., 1986, Production of 10Be and 26Al by cosmic rays in terrestrial quartz in situ and implications for erosion rates: Nature, v. 319, no. 6049, p. 134–136.
- Nishiizumi, K., Klein, J., Middleton, R., and Craig, H., 1990, Cosmogenic 10Be, 26Al, and 3He in olivine from Maui lavas: Earth and Planetary Science Letters, v. 98, no. 3–4, p. 263–265.
- Nishiizumi, K., Imamura, M., Caffee, M.W., Southon, J.R., Finkel, R.C., and McAninch, J., 2007, Absolute calibration of 10Be AMS standards: Nuclear Inst. and Methods in Physics Research, B, v. 258, no. 2, p. 403–413.
- Ouimet, W.B., Whipple, K.X., and Granger, D.E., 2009, Beyond threshold hillslopes: Channel adjustment to base-level fall in tectonically active mountain ranges: Geology, v. 37, p. 579–582.
- Palumbo, L., Hetzel, R., Tao, M., and Li, X., 2009, Topographic and lithologic control on catchment-wide denudation rates derived from cosmogenic 10Be in two mountain ranges at the margin of NE Tibet: Geomorphology, v. 117, p. 130–142.
- Peizhen, Z., Molnar, P., and Downs, W.R., 2001, Increased sedimentation rates and grain sizes 2–4 Myr ago due to the influence of climate change on erosion rates: Nature, v. 410, p. 891–897.
- Reuter, J.M., 2005, Erosion rates and patterns inferred from cosmogenic 10Be in the Susquehanna River basin [M.S. Thesis]: Burlington, University of Vermont, 172 p.
- Riebe, C.S., Kirchner, J.W., Granger, D.E., and Finkel, R.C., 2001a, Minimal climatic control on erosion rates in the Sierra Nevada, California: Geology, v. 29, no. 5, p. 447–450.
- Riebe, C.S., Kirchner, J.W., Granger, D.E., and Finkel, R.C., 2001b, Strong tectonic and weak climatic control of long-term chemical weathering rates: Geology, v. 29, no. 6, p. 511–514.
- Safran, E.B., Bierman, P.R., Aalto, R., Dunne, T., Whipple, K.X., and Caffee, M., 2005, Erosion rates driven by channel network incision in the Bolivian Andes: Earth Surface Processes and Landforms, v. 30, no. 8, p. 1007–1024.
- Saunders, I., and Young, A., 1983, Rates of surface processes on slopes, slope retreat, and denudation: Earth Surface Processes and Landforms, v. 8, p. 473–501.
- Schaller, M., von Blanckenburg, F., Hovius, N., and Kubik, P.W., 2001, Large-scale erosion rates from in situ-produced cosmogenic nuclides in European river sediments: Earth and Planetary Science Letters, v. 188, p. 441–458.
- Small, E.E., Anderson, R.S., Repka, J.L., and Finkel, R., 1997, Erosion rates of alpine bedrock summit surfaces deduced from in situ 10Be and 26Al: Earth and Planetary Science Letters, v. 150, no. 3–4, p. 413–425.
- Sullivan, C.L., 2007, 10Be erosion rates and landscape evolution of the Blue Ridge Escarpment, southern Appalachian Mountains: University of Vermont, 76 p.
- Syvitski, J.P.M., Vorosmarty, C.J., Kettner, A.J., and Green, P., 2005, Impact of Humans on the Flux of Terrestrial Sediment to the Global Coastal Ocean: Science, v. 308, p. 376–380.
- Trimble, S.W., 1977, The fallacy of stream equilibrium in contemporary denudation studies: American Journal of Science, v. 277, p. 876–887.
- von Blanckenburg, F., 2005, The control mechanisms of erosion and weathering at basin scale from cosmogenic nuclides in river sediment: Earth and Planetary Science Letters, v. 23, no. 7, p. 462–479.
- von Blanckenburg, F., Hewawasam, T., and Kubik, P.W., 2004, Cosmogenic nuclide evidence for low weathering and denudation in the wet, tropical highlands of Sri Lanka: Journal of Geophysical Research, v. 109, no. F3.
- Walling, D.E., 1983, The sediment delivery problem: Journal of Hydrology, v. 65, no. 1–3, p. 209–237.
- Wilkinson, M.T., Chappell, J., Humphreys, G.S., Fifield, K., Smith, B., and Hesse, P., 2005, Soil production in heath and forest, Blue Mountains, Australia: Influence of lithology and palaeoclimate: Earth Surface Processes and Landforms, v. 30, no. 8, p. 923–934.
- Wittmann, H., von Blanckenburg, F., Guyot, J.L., Maurice, L., and Kubik, P.W., 2009, From source to sink: Preserving the cosmogenic 10Be-derived denudation rate signal of the Bolivian Andes in sediment of the Beni and Mamoré foreland basins: Earth and Planetary Science Letters, v. 288, p. 463–474.
- Zeitler, P.K., Meltzer, A.S., Koons, P.O., Craw, D., Hallet, B., Chamberlain, C.P., Kidd, W.S.F., Park, S.K., Seeber, L., Bishop, M., and Shroder, J., 2001, Erosion, Himalayan geodynamics, and the geomorphology of metamorphism: GSA Today, v. 11, no. 1, p. 4–9.

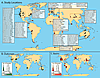 Figure 1
Figure 1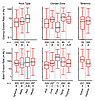 Figure 3
Figure 3 Figure 4
Figure 4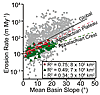 Figure 5
Figure 5