Full Text View
Volume 29 Issue 2 (February 2019)
GSA Today
Article, pp. 4-10 | Abstract | PDF (2MB)
A More Informative Way to Name Plutonic Rocks
Cover Image
Table of Contents
- Introduction
- Rock Names, Necessary and Superfluous
- A Simpler, Quantitative Approach
- Modified IUGS Method for Classification of Plutonic Rocks
- Summary
- Acknowledgments
- References Cited
Search Google Scholar for
Search GSA Today
Abstract
The International Union of Geological Sciences (IUGS) system for rock classification, introduced more than 40 years ago, has served geologists well but suffers from the problem of dividing a continuum of rock compositions into arbitrary bins. As a result, closely related rocks can be given unrelated names (e.g., granodiorite and tonalite), and the names themselves, which were generally derived from the names of places or people, rarely contribute to understanding the processes that generate the diversity of igneous rocks. Here we propose a quantitative modification to the IUGS system that reduces the number of distinct names but more effectively communicates the inherent variability of plutonic rocks. The system recognizes that mapped plutonic rock units are characterized by recognizable textures and mineral assemblages, but that mineral proportions within those units can be highly variable. Adding quantitative data to rock names is an important step toward moving geologic field observations into quantitative digital form and preparing them for advanced data mining and analysis.
One thing quarks do have going for them: all their names are simple—something chemists, biologists, and especially geologists seem incapable of achieving when naming their own stuff. —Neil deGrasse Tyson, Astrophysics for People in a Hurry
Manuscript received 11 Sept. 2018. Revised manuscript received 27 Nov. 2018. Manuscript accepted 30 Nov. 2018. Posted 9 Jan. 2019.
© The Geological Society of America, 2019. CC-BY-NC.
Introduction
Why do we bother to name rocks? One answer among many is that rock categories can efficiently convey important information about a geologic setting just as biological categories can convey the same for ecosystems. Say “zebra” to a biologist and they will likely think “African savanna”; say “granodiorite” to a geologist and they will likely think “subduction zone.” However, the sheer number of igneous rock names presents a formidable entry barrier to students of the field. In a recent undergraduate textbook, Winter (2010, p. 32) lists 157 common igneous rock names, many of them unknown to practicing petrologists. Say “kugdite” to a geologist and you will likely get a puzzled stare.
Classification of igneous rocks has occupied and irritated petrologists for centuries. Unlike biological classifications, which can place organisms into discrete categories, rock classifications place sharp boundaries between objects that are completely gradational. A biologist can classify something definitively as a dog or cat, knowing that there are no doggish cats or cattish dogs, but a petrologist cannot do so—there are plenty of granodioritic granites and granitic granodiorites (Fig. 1). Thus, any classification based on discrete categories will split continuously variable rock compositions at arbitrary boundaries.
An international effort to systematize the nomenclature of plutonic igneous rocks was started in the 1960s under the leadership of Swiss petrologist Albert Streckeisen, and summaries of this work (e.g., Streckeisen, 1974, 1976; LeBas and Streckeisen, 1991) are the standard references for current nomenclature. The principal classification is based on a double triangle (Fig. 2); this diagram, appropriate for rocks with 10% or more quartz or feldspathoid minerals plus feldspars, uses the modal (volume) proportions of quartz (Q), alkali feldspar (A), plagioclase (P), and feldspathoids (F) to name rocks.
The International Union of Geological Sciences (IUGS) commission aimed to simplify the nomenclature, eliminate synonymic terms (e.g., adamellite = quartz monzonite), and come up with fields and corresponding names that are consistent with general usage. The IUGS method relies on two parameters, the modal percentage of quartz or feldspathoid minerals (horizontal lines), and the ratio of alkali feldspar to plagioclase (lines radiating from the quartz and feldspathoid apices). These values are easy to estimate in thin section, although less so in the field, where the plagioclase/alkali feldspar distinction can be subtle. In contrast, the modal proportions of mafic minerals and their sum (color index) are generally easy to estimate in the field and diagnostic of a given rock unit, although these are not used in the IUGS system. The IUGS diagram provides a convenient way to assign a standardized name once the mode has been estimated, and this is both a strength and a significant problem.
As an example of the problems that this kind of classification can cause, consider the data in Figure 3, taken from Bateman (1992). Modal data from the well-known Cathedral Peak Granodiorite of Yosemite National Park in California, USA (Fig. 1), are split rather evenly between the granite and granodiorite fields. Thus, any random hand sample or outcrop of the Cathedral Peak pluton might be a granite or a granodiorite or straddle the arbitrary boundary between them. This unit was designated a granodiorite because one or the other name had to be chosen, even though the pluton includes both. The nearby El Capitan Granite (Fig. 1) is also more-or-less evenly divided between the granite and granodiorite fields (with several points in the tonalite field), but it is officially a granite. Rocks of the Kuna Crest suite, a set of medium-grained rocks with high color index, scatter over the granodiorite, tonalite, quartz monzodiorite/quartz monzogabbro, and quartz diorite/quartz gabbro fields. This sort of artificial separation-by-name of closely related rocks is an unfortunate consequence of fitting observations into arbitrarily defined boxes.
Figure 3 also shows that the color indices of rocks called El Capitan Granite range from near zero to more than 20, an important point to which the name “granite,” as defined by the IUGS system, gives no indication. In general, color index increases moving away from the center of the quartz-alkali feldspar-plagioclase (QAP) triangle, toward plagioclase (Fig. 4). The abundances and identities of the mafic phases (e.g., biotite, hornblende, titanite) are typically where the geochemical action is, and yet the IUGS classification has no provision for this.
Thus, the current system of igneous rock nomenclature suffers from several shortcomings: (1) it conceals the variability of igneous rocks at the map unit scale with restrictive names; (2) it lacks important information about the mineralogy of the rocks at scales ranging from pluton to hand sample; (3) it is burdened by unnecessary names that, by themselves, tell nothing; and (4) the quantitative data used to derive a name are largely discarded once the name is applied. This last point must be addressed if we are to move field observations from “dark data” (Heidorn, 2008), buried in field notebooks, into sharable digital form (Walker et al., in press).
Bowen (1928) foresaw the problems with using mineral abundances as a basis of classification. Noting an analogy between mineral assemblages and life assemblages, he said:
How artificial a classification of faunas would be which was based on the ratio of foxes to hares, of hares to moles and so on! To be sure it is by no means accidental that the ratio of hares to foxes is 10 in a certain area and only 2 in another, but as compared with the broad factors controlling life in the two areas it is relatively accidental… So it is not accidental that a rock is nearly pure olivine here and only 75 per cent olivine a few feet distant, but it is relatively accidental and should not be made a fundamental factor in classification.
Bowen clearly recognized the problems inherent in classifications based on mineral proportions, and yet that is the system with which we live. We contend that an improved system could address the shortcomings of the IUGS system by:
- using a more restricted set of names, because restricting the subdivision of names allows each name to encompass greater modal variation;
- allowing for overlap between rock categories; and
- including quantitative information about modal mineralogy at scales for which quantification is appropriate.
Rock Names, Necessary and Superfluous
There are thousands of igneous rock names (e.g., Johannsen, 1932, and accompanying volumes), but most samples described in the literature are covered by just one or two dozen. We compiled the number of citations in GeoRef mentioning 19 of the most common IUGS names over the period 1970–2018. “Granite” made up just under half of the total number of citations (~223,000) in this list, and the names were distributed as in Figure 5. The first nine names account for 90% of the citations (allowing for multiple counting of citations listing more than one name).
As is common with textual data, rock names roughly obey Zipf’s Law (Aitchison et al., 2016), which states that the frequency of a given word is inversely proportional to its frequency rank. There are ~50,000 rock names in the North American Volcanic and Intrusive Rock database (NAVDAT) of western North American igneous rocks (Walker et al., 2006), 105 of them unique. The first 18 names make up 90% of the samples; the remaining 87 names are rarely applied. We contend that these surplus names (e.g., sannaite, malignite), although locally useful, are largely noise that obscures the signals of petrologic processes.
It is somewhat bewildering that petrologists have used modal mineralogy to classify plutonic rocks for a century, and yet these data are rarely recorded in digital databases. In NAVDAT, only ~5% of the analyses have associated modal data, and one-third of those are from just two sources.
A Simpler, Quantitative Approach
We propose the following classification methods for three major groups of rocks: quartz/feldspathoid- + feldspar-bearing, ultramafic, and gabbroic. We do not propose equivalent schemes for other igneous rock groups (e.g., lamprophyres, carbonatites, agpaites), but a similar approach could be applied to all plutonic rocks, and the same reasoning could be applied to chemical classifications (e.g., total alkalis- silica) for volcanic rocks.
Our approach borrows conceptually from the International Union for Pure and Applied Chemistry (IUPAC) system for naming organic compounds. In the 1950s, nomenclature for organic compounds was bloated and tangled. Names and properties of thousands of known organic compounds were compiled originally by Beilstein (1881), much as names and properties of igneous rocks were compiled by Johannsen (1938, and accompanying volumes). The Beilstein compilation includes the name of the compound and assigns it a unique number. However, the common name and Beilstein number provide limited information about the nature of a compound.
IUPAC therefore set out to create a nomenclatural scheme that would be more systematic and informative. The IUPAC system consists of a set of root names that correspond to chemically and structurally simple organic molecules (e.g., the alkanes methane, ethane, propane, etc.), preceded by modifiers that identify and describe the spatial arrangement of atoms added to the root molecule to form a particular compound. For example, the compound on which the octane rating system of gasoline is based, isooctane, is 2,2,4 trimethylpentane in the IUPAC system. When decoded, this provides a complete description of the molecule.
Plutonic rocks are a chemical continuum rather than a collection of discrete compounds; therefore, a system that is analogous to IUPAC organic nomenclature cannot be constructed. However, a broadly similar approach can achieve much the same goals.
We suggest that an optimal system of plutonic rock names will use a small number of root names along with the modal proportions of the minerals used in the classification. Each root name corresponds to a particular combination of major minerals and thus indicates the relevant classification triangle or tetra-hedron. The absolute minimum number of root names is four: “granite” for rocks classified on the basis of quartz, alkali feldspar, and plagioclase; “foid syenite” or some other moniker for those dominated by feldspathoids, alkali feldspar, and plagioclase; “peridotite” for olivine, orthopyroxene, and clinopyroxene; and “gabbro” for plagioclase, olivine, orthopyroxene, and clinopyroxene. In this extreme rendering of our approach, the 27 fields in the Streckeisen double triangle are replaced by two root names, granite for the upper triangle and foid syenite for the lower triangle.
The simplicity of the extreme approach is appealing, but we see reasons for a less radical trimming of the list of recognized rock names. First, some combinations of names trace a process; e.g., lherzolite, harzburgite, and dunite trace the composition of the mantle residue of basalt extraction. Second, a small number of root names can provide a convenient shorthand for differences between related rocks that are awkward to express by differences in the mineral proportions. Finally, allowing a given set of mineral components to map into more than one rock name permits the boundaries between the rock names to be fuzzy, reflecting the real variability of the rocks noted by Bowen (1928). This inherent flexibility can allow the rock names that are retained to emerge from their actual usage rather than being imposed by a committee.
We therefore propose an approach to naming rocks that consists of a root name preceded by a vector of mineral abundances. As this is a new system, we do not claim to know the optimal balance between reducing the number of root names for simplicity and retaining root names because they are sufficiently useful to warrant it. The following examples of our approach therefore are meant to be illustrative rather than definitive; if the system is adopted, optimal names will arise organically rather than by fiat.
Finally, there are many reasons that root names alone should continue to be used to name map-scale bodies of plutonic rock. Addition of a numerical vector to a root name is intended only to be used at the scale of individual samples from a map-scale body. Indeed, by making the boundaries around rock names fuzzy, usage in pluton names and rock names becomes more consistent.
Modified IUGS Method for Classification of Plutonic Rocks
The following procedure involves the same observations needed to classify a rock with the IUGS method, and thus the full IUGS name can always be applied. All percentages are modal (volume %).
Rocks with Quartz + Feldspars >10% (Upper Half of IUGS Diamond)
- Estimate the proportions of quartz (Q), alkali feldspar (A), plagioclase (P), and mafic minerals (M), and the identities of mafic minerals and accessories (example: 20,20,50,10; biotite, hornblende, titanite).
- Assign a root name based on where the QAP estimate, normalized to 100, falls on the upper triangle in Figure 6 (example: granodiorite).
- Prefix the rock name with unnormalized QAP; e.g., 20,20,50. The proportion of mafic minerals (color index) is implicit in these numbers as 100 minus their sum (example: 20,20,50 granodiorite; color index is 10).
- Prefix the resulting name with relevant mafic minerals, using defined abbreviations if desired. The prefix should list these in increasing abundance so that the most abundant is closest to the root name (Shelley, 1993, p. 7) (example: hbl-bio 20,20,50 granodiorite).
- Important accessory minerals can be denoted by, for example, titanite- bearing or ttn-bearing (example: ttn-bearing hbl-bio 20,20,50 granodiorite).
Note that these steps are identical to the IUGS method except that there are far fewer bins in which to put the rocks (six versus sixteen). The bins simply indicate broad QAP proportions. For example, granites and granodiorites are quartz-rich and distinguished broadly by alkali feldspar > plagioclase or plagioclase > alkali feldspar, respectively. Syenites are rich in alkali feldspar and poor in plagioclase + quartz. Diorites are rich in plagioclase and poor in alkali feldspar + quartz, and so on.
For map scale, nomenclature likely skips Step 3 because the modal variation at that scale is too variable for quantification. Accordingly, the Cathedral Peak Granodiorite mentioned earlier would be just that, or the Cathedral Peak Biotite Granodiorite to reflect the dominant mafic mineral. This does not directly address the fact that the Cathedral Peak body includes both granodiorites and granites as defined by IUGS boundaries. However, the recognition that a granodiorite is defined as a quartz-rich rock, with generally (but not necessarily exclusively) plagioclase > alkali feldspar, is an improvement in representing the nature of the pluton. Addition of the mafic mineralogy to the name significantly advances one’s knowledge of what to expect in the field.
A particular hand sample of the Cathedral Peak pluton might be called a hornblende-biotite 30,20,45 granodiorite, indicating a color index of 5 with biotite > hornblende. The variation in mineralogy in the El Capitan pluton could be described as a range from biotite 30,50,20 granite to hornblende-biotite 25,10,55 granodiorite. This expresses the variations observed in the felsic and mafic mineralogy and color index far better than the unqualified names.
Rocks with Feldspathoid(s) + Feldspars >10% (Lower Half of IUGS Diamond)
Classification of feldspathoid-bearing rocks is the same as with quartz-bearing rocks except that the identity of the feldspathoid(s) replaces “foid” (e.g., nepheline syenite rather than foid syenite).
Ultramafic Rocks
Olivine-pyroxene rocks with <10% felsic minerals are named via the olivine- orthopyroxene-clinopyroxene (OOC) triangle (Fig. 7). The same simplification principles apply to these rocks: estimate mineral proportions and then name the rock with these numbers and the simplified, blurred boundary classification in Figure 7. Preface the name with other important minerals such as garnet or spinel; their proportion is 100 minus the sum of OOC.
Gabbroic Rocks
Gabbroic rocks can be classified using a tetrahedron with apices of plagioclase, olivine, orthopyroxene, and clinopyroxene (POOC; Fig. 8). The base of the tetrahedron is the OOC triangle of Figure 7; the apices are anorthosite, dunite, orthopyroxenite, and clinopyroxenite; troctolite lies along the plagioclase- olivine edge, and the interior is gabbro or norite depending on whether the dominant pyroxene is clinopyroxene or orthopyroxene. Hybrid names, such as gabbronorite, and qualified names, such as olivine gabbro, are unnecessary (but can be used if desired) when the defining mineralogy is given in the name (e.g., 50,10,20,20 gabbro).
Examples
- A rock has 20% quartz, 20% K-feldspar, 50% plagioclase, with the remainder (10%) mafic minerals consisting of biotite > hornblende. The root name would be granodiorite, and the rock would be a hbl-bio 20,20,50 granodiorite.
- A shonkinite (Johannsen, 1932, p. 355) contains 3% quartz, 8% orthoclase, 22% plagioclase, 65% hornblende, and 2% accessories. This would be a hbl 3,8,22 monzonite. The sum of Q, A, and P is only 33, implying a large amount of hornblende ± other phases.
- A “leucolitchfieldite” from Johannsen (1938, p. 181) contains 16% microcline, 55% plagioclase, 18% nepheline, 8% muscovite, and 1% each magnetite and biotite. This would be an 18,16,55 nepheline syenite or a musc 18,16,55 nepheline syenite.
- Boyd and McCallister (1976) gave a peridotite mode as 59% olivine, 11% orthopyroxene, 20% clinopyroxene, and 10% garnet. This rock would be a garnet 59,11,20 lherzolite.
- Boudreau (1988) listed modal mineralogy of rocks from the Stillwater Complex as Table 1.
Complications
There are many details. For example, it is common in granitoids that the feldspars are difficult to distinguish in the field; in such cases they can be lumped, with only two numbers reported, as biotite 35,60 granite. Modal data can be determined with varying levels of precision. Field estimates might be good to only the nearest 10%, whereas microscopic estimates can be good to a percent; the approximate precision should always be stated. A feldspathoidal rock might contain two or more important feldspathoids, as in 30,20,40 sodalite-nepheline syenite, indicating sodalite + nepheline = 30 and sodalite < nepheline.
Summary
There are several advantages to this method of naming plutonic rocks.
- It allows for overlap of names such as “granite” and “granodiorite.” These names are redundant of the quantitative information and merely serve as a guide to the appropriate classification triangle or tetrahedron and to the overall rock type.
- The abundances of the determinative minerals are given directly in the name, and the QAP/FAP/OOC/POOC parameters can be calculated from the name.
- Thus, everything needed to derive the standard IUGS classification is in the name.
- For quartz/feldspathoid rocks, the color index is implicit in the name; for gabbros, this gives the proportion of minerals other than plagioclase, pyroxenes, and olivine; for ultramafic rocks, this exercise gives the proportion of minerals other than olivine and pyroxene, such as garnet or spinel. Such information is neglected by the IUGS naming scheme.
- There are many fewer rock names and field boundaries to commit to memory, freeing the mind to think about processes rather than classification.
- Freight trains of syllables in hybrid names such as quartz monzodiorite are avoided. We contend that 10,20,60 diorite is both less cumbersome and more informative than quartz monzodiorite.
- Quantitative modal and mineralogical data become part of the rock name, allowing for more complete and easily accessible information in databases, which in turn allows for new scientific opportunities in data mining (e.g., Hazen et al., 2011).
We hope that this modification of the venerable IUGS scheme will be adopted in order to simplify and take the stress out of naming plutonic rocks, with the added benefit of adding significant quantitative information that can be easily assimilated in digital form.
Acknowledgments
We thank editor Mihai Ducea for encouraging this work, Jade Star Lackey, Doug Walker, Ryan Mills, Andy Barth, and Alan Boudreau for comments on the manuscript, and Bob Hazen and an anonymous reviewer for helpful reviews. This work is supported by National Science Foundation grant EAR-1551990 to Glazner.
References Cited
- Aitchison, L., Corradi, N., and Latham, P.E., 2016, Zipf’s law arises naturally when there are underlying, unobserved variables: PLoS Computational Biology, v. 12, e1005110, https://doi.org/10.1371/journal.pcbi.1005110.
- Bateman, P.C., 1992, Plutonism in the central part of the Sierra Nevada batholith, California: U.S. Geological Survey Professional Paper 1483, 186 p.
- Bateman, P.C., Dodge, F.C.W., and Bruggman, P.E., 1984, Major oxide analyses, CIPW norms, modes, and bulk specific gravities of plutonic rocks from the Mariposa 1 degrees by 2 degrees sheet, central Sierra Nevada, California: U.S. Geological Survey Open-File Report 84-0162, 59 p.
- Bateman, P.C., Chappell, B.W., Kistler, R.W., Peck, D.L., and Busacca, A.J., 1988, Tuolumne Meadows Quadrangle, California; analytic data: U.S. Geological Survey Bulletin 1819, 43 p.
- Beilstein, F.K., 1881, Handbuch der organischen Chemie: Hamburg, Germany, Verlag von Leopold Voss, 2200 p.
- Boudreau, A.E., 1988, Investigations of the Stillwater Complex. IV. The role of volatiles in the petrogenesis of the J-M Reef, Minneapolis adit section: Canadian Mineralogist, v. 26, p. 193–208.
- Bowen, N.L., 1928, The Evolution of the Igneous Rocks: Princeton, New Jersey, Princeton University Press, 333 p.
- Boyd, F.R., and McCallister, R.H., 1976, Densities of fertile and sterile garnet peridotites: Geophysical Research Letters, v. 3, p. 509–512, https://doi.org/10.1029/GL003i009p00509.
- Hazen, R.M., Bekker, A., Bish, D.L., Bleeker, W., Downs, R.T., Farquhar, J., Ferry, J.M., Grew, E.S., Knoll, A.H., Papineau, D., Ralph, J.P., Sverjensky, D.A., and Valley, J.W., 2011, Needs and opportunities in mineral evolution research: The American Mineralogist, v. 96, p. 953–963, https://doi.org/10.2138/am.2011.3725.
- Heidorn, P.B., 2008, Shedding light on the dark data in the long tail of science: Library Trends, v. 57, p. 280–299, https://doi.org/10.1353/lib.0.0036.
- Johannsen, A., 1932, A Descriptive Petrography of the Igneous Rocks, Volume II: Chicago, University Press, 428 p.
- Johannsen, A., 1938, A Descriptive Petrography of the Igneous Rocks, Volume IV: Chicago, University Press, 523 p.
- Le Bas, M.J., and Streckeisen, A.L., 1991, The IUGS systematics of igneous rocks: Journal of the Geological Society, v. 148, p. 825–833, https://doi.org/10.1144/gsjgs.148.5.0825.
- Shelley, D., 1993, Igneous and Metamorphic Rocks under the Microscope: Classification, Textures, Microstructures and Mineral Preferred-Orientations: New York, Chapman & Hall, 445 p.
- Streckeisen, A., 1974, Classification and nomenclature of plutonic rocks recommendations of the IUGS subcommission on the systematics of Igneous Rocks: Geologische Rundschau, v. 63, p. 773–786, https://doi.org/ 10.1007/BF01820841.
- Streckeisen, A., 1976, To each plutonic rock its proper name: Earth-Science Reviews, v. 12, p. 1–33, https://doi.org/10.1016/0012-8252(76)90052-0.
- Walker, J.D., Bowers, T.D., Black, R.A., Glazner, A.F., Farmer, G.L., and Carlson, R.W., 2006, A geochemical database for western North American volcanic and intrusive rocks (NAVDAT), in Sinha, A.K., ed., Geoinformatics: Data to Knowledge: Geological Society of America Special Paper 397, p. 61–71, https://doi.org/10.1130/2006.2397(05).
- Walker, J.D., Tikoff, B., Newman, J., Clark, R., Ash, J.M., Good, J., Bunse, E.G., Möller, A., Kahn, M., Williams, R., Michels, Z., Andrew, J.E., and Rufledt, C., 2019, StraboSpot data system for structural geology: Geosphere, https://doi.org/ 10.1130/GES02039.1 (in press).
- Winter, J.D., 2010, An Introduction to Igneous and Metamorphic Petrology: New York, Prentice Hall, 702 p.


 Figure 1
Figure 1 Figure 2
Figure 2 Figure 3
Figure 3 Figure 4
Figure 4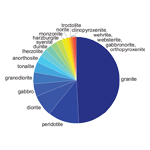 Figure 5
Figure 5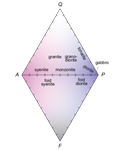 Figure 6
Figure 6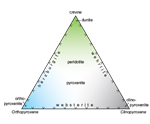 Figure 7
Figure 7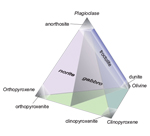 Figure 8
Figure 8 Table 1
Table 1